Groovy Gravity Processing

Joshua (a coworker) and I have been talking about gravity simulation for a while, and this week I threw together a very simple model to do exactly that.  This grew out of a game called Flotilla that he came across somewhere and has been working with the developer to add a network multiplayer mode.  Flotilla, however, doesn't have a concept of gravity, and doesn't really have an explicit concept of mass either, except the implicit stuff in it's acceleration constraints.

Gravity, however, is kind of nasty to work with (from a computational perspective), particularly in a game situation (where you want realism, but not so real the game play sucks).  Fortunately, it's also exactly the kind of thing that I enjoy wasting my free time playing with.  So I threw together a simple model in Groovy, including a little type system and DSL to help keep my numbers straight.

So now when I divide a Force by a Mass, I'll get an Acceleration back.  Or if I multiply an Acceleration by a Time, I'll get a Velocity.  This was a huge win.  In the world of paper calculations, you don't do just arithmetic, you do unit algebra as well, which helps you ensure your answer makes sense (e.g., if you solve for velocity and get units of "meters per kilogram second", you screwed up somewhere).  But with a computer you don't have units, so I employed a simple type system to afford the same check I'd usually get from unit algebra.  And Groovy makes it remarkably easy to create both an expressive type system and a simple syntax (via operator overloading).

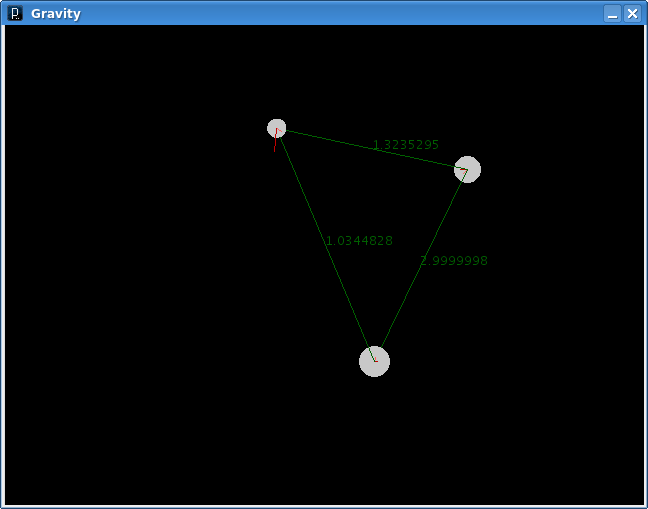
Then I hacked up Processing ever so slightly so I could implement a PApplet in Groovy and avoid the compilation step, and built a simple viewer for the model.  Emphasis on "simple".  Here's a capture with three bodies:

The bodies' sizes represent their relative mass, the green lines represent gravitation between them, the red lines are the velocity vector (per body), and the pink lines are acceleration (also per body).  Here's a few seconds later in the same simulation:

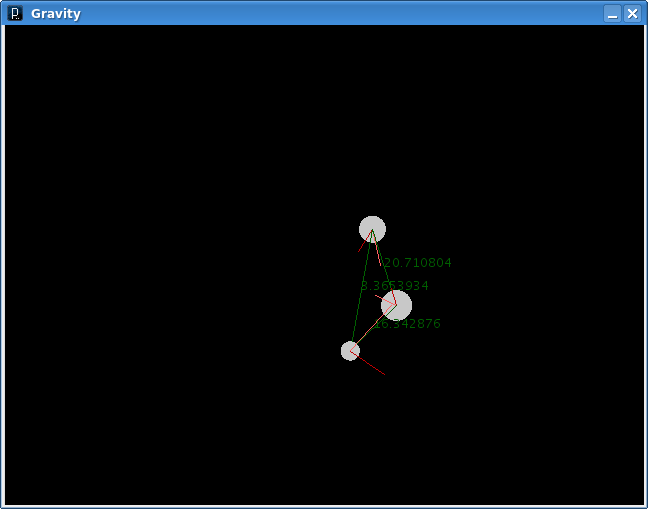
Now, because the bodies are far closer, the forces between them are much greater, which is going to result in a couple fairly impressive slingshots in a moment.  They've also picked up a fair amount of speed, though their active acceleration has surpassed their velocities (i.e., slingshots are imminent).  Here's after the slingshots have happened:

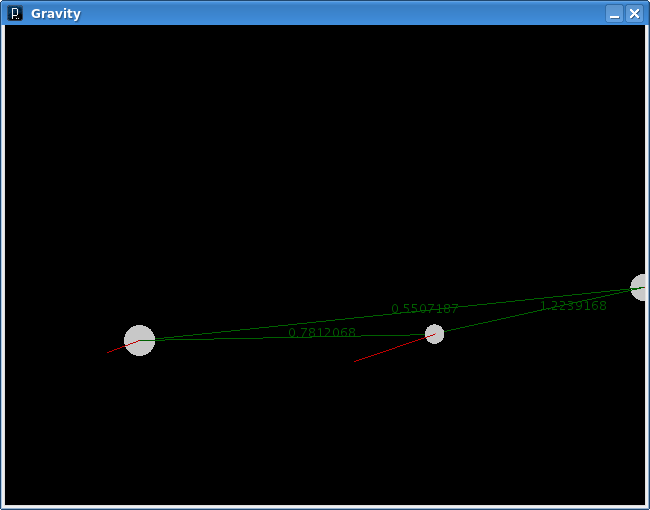
After the two larger bodies slingshotted around each other, the two smaller bodies did the same thing, resulting in a rapidly expanding model.  As you can see the forces are falling away, though the smallest and largest bodies will soon meet up and cross paths.  The velocity of the little one is high enough that the big one can't slow it down enough to do more than deflect it upward a bit.

Processing again completely delivered on it's promise of providing a remarkably simple way to sketch out visual stuff.  Simple event handling, simple setup, a simple draw loop, and solid primitives.  I need to do a little mucking about, but adding 3D support (which the model handles, but the viewer doesn't) will be similarly trivial: flip the "use 3D" bit, and add 'z' coordinates from the model in the various calls.  Very nice, especially when coupled with the Groovy syntax and capabilities.

An interesting project, though we'll see how generally useful.  Code, of course, is available from SVN.  It's a single Eclipse project, including Groovy, Processing, the hacked PApplet (from Processing), the model and the viewer applet.  Check it out and run driver.groovy to see it in action.  While running SPACE will pause/unpause the action, though there is currently no way to rewind/reset the simulation.  If you don't want to check out the project, you can browse it directly.  The interesting bits are in the /src/com/barneyb/gravity/ package.